HEMPEL, C. 2004

Carl Hempel (1905-1997) est un philosophe des sciences et une figure majeure du positivisme logique /empirisme logique au xx^e siècle. Il est particulièrement connu pour l’élaboration du modèle « déductif-nomologique », qui a été considéré comme le modèle standard de l’explication scientifique durant les années 1950 et 1960.  Dans ce modèle, Hempel a tenté de formaliser le procédé de la science classique. Selon cette manière de voir, les conditions initiales de l’expérience sont raccordées à des lois générales (aspect nomologique). À partir de là, se déduisent (aspect déductif) certains faits particuliers produits par l’expérience en question.

L’explication insère le fait dans la régularité donnée par des lois, ce qui permet de le prévoir de manière assurée pour peu que les conditions initiales particulières soient connues. Autrement dit, on déduit la proposition élémentaire décrivant le fait de plusieurs propositions générales exprimant des lois. Nous avons là une définition simple et intéressante, car elle spécifie et différencie de manière nette l’activité scientifique mais, problème essentiel, elle ne dit pas comment les lois générales sont obtenues.

Les lois générales une fois établies, il est possible, à partir d’un certain nombre de données empiriques, d’en conclure à un énoncé valide et prédictif.

 

Les Éléments d’épistémologie (2004) présentent une initiation aux thèmes principaux de l’épistémologie telle qu’elle est conçue dans la tradition de l’école de Vienne. Je retiendrai essentiellement le chapitre 7 consacré à la formation des concepts en se posant la question de l’articulation entre la manière dont Hempel conçoit ce processus et la façon dont le logicisme présente les démonstrations sous forme de schématisations.

 

Position de Carl Hempel

Selon Hempel il existe trois types de définitions : les définitions descriptives, les définitions stipulatives et les définitions opératoires.

Dans la définition descriptive A (definiendum) a la même définition de B (definiens)

Par exemple : « père (A) a la même signification que parent mâle (B) »

De telles définitions analytiques ont pour but d’analyser la signification admise d’un terme et de le décrire à l’aide d’autres termes dont la signification doit être comprise si l’on veut que la définition fasse l’affaire. Elles spécifient l’étendue des applications ou extension. On peut les dire plus ou moins exactes et même vraies ou fausses.

Dans la définition stipulative on donne à A la même définition qu’à B. La signification du terme est construite au moyen de termes qui sont déjà compris. 

Par exemple : « densité (A) est l’abréviation de masse en grammes par centimètre cube (B) ».

Il peut sembler qu’idéalement chaque terme utilisé dans une théorie scientifique devrait être défini avec précision. Mais c’est là une impossibilité logique ; car, après avoir formulé une définition pour un terme, nous aurions ensuite à définir à leur tour chacun des termes utilisés pour définir ces derniers et ainsi de suite, en évitant les « cercles », c’est-à-dire définir un terme à l’aide de certains de ceux qui précèdent dans la chaîne. Dans toute théorie scientifique il existe donc une série de termes que l’on appelle primitifs ou préthéoriques qui ne reçoivent aucune définition à l’intérieur du système.

La définition opératoire est plus exigeante. Selon les travaux de P. W. Bridgman la signification de chaque terme scientifique doit pouvoir être déterminée en spécifiant une opération de vérification bien définie qui lui fournit un critère d’application.

Percy Williams Bridgman (1881-1961) est un physicien américain qui a écrit sur la logique de la physique moderne (1927).

De tels critères sont souvent appelés définitions opératoires. Le but des définitions opératoires est d’assurer la testabilité objective de tous les énoncés scientifiques. Un terme scientifique doit ainsi permette de dériver des implications vérifiables sans équivoque à partir des hypothèses où ces termes figurent.

Par exemple une version opérationaliste explicite de la définition de l’aimant pourrait être :« Un aimant peut être une barre de fer ou d’acier qui attire à ses extrémités des grains de limaille de fer ». Mais il peut être également autre chose. Ou, autrement formulé :

« Si des grains de limaille de fer sont attirés par les extrémités d’une barre de fer ou d’acier, alors cette barre est un aimant ».

 

Relations avec le logicisme

Quelles relations établir entre ces trois types de définitions et la façon dont le logicisme mobilise des concepts ? Trois questions se posent dans ce domaine.

 

Question 1. Comment articuler la réflexion de Hempel sur la formulation des concepts et la façon dont le logicisme présente les démonstrations sous forme de schématisations ?

La question de la formation des concepts nous semble s’organiser selon plusieurs axes perpendiculaires aux chaînages des démonstrations du logicisme et constituer un aspect complémentaire, indispensable, des démonstrations, une question en effet peu abordée par le logicisme. Cette question touche à la fois les définitions descriptives et les définitions stipulatives ainsi que les définitions opératoires. Dans le domaine anthropologique Alain Testart s’est par exemple attaché à préciser un grand nombre de concepts tant au niveau social que politique.

 

Question 2. L’analogie que l’on constate entre les définitions dites opératoires et les formulations dites de transfert d’attribut du logicisme révèle-t-elle une situation épistémologique identique ?

La définition opératoire peut prendre une forme si Pi alors Pi+1 comparable à celle introduite par le logicisme (cf. ci-dessus). Cette définition permet de tester la pertinence d’une définition descriptive sur la réalité.

On peut alors se poser la question suivante : la définition opératoire : « Si des grains de limaille de fer sont attirés par les extrémités d’une barre de fer ou d’acier, alors cette barre est un aimant ».

Est-elle formellement identique au transfert d’attribut :

« Si j’observe un gros oiseau sur une main gantée alors il s’agit d’un faucon »

ou autrement formulé :

« Un faucon peut être un gros oiseau sur une main gantée » ? Mais il peut être également autre chose.

Ces formulations permettent effectivement de procéder à des tests de validation ou d’invalidation sur des corpus de références divers, une situation qui renforce l’analogie constatée entre définition opératoire et logique du transfert d’attribut (fig. 1).

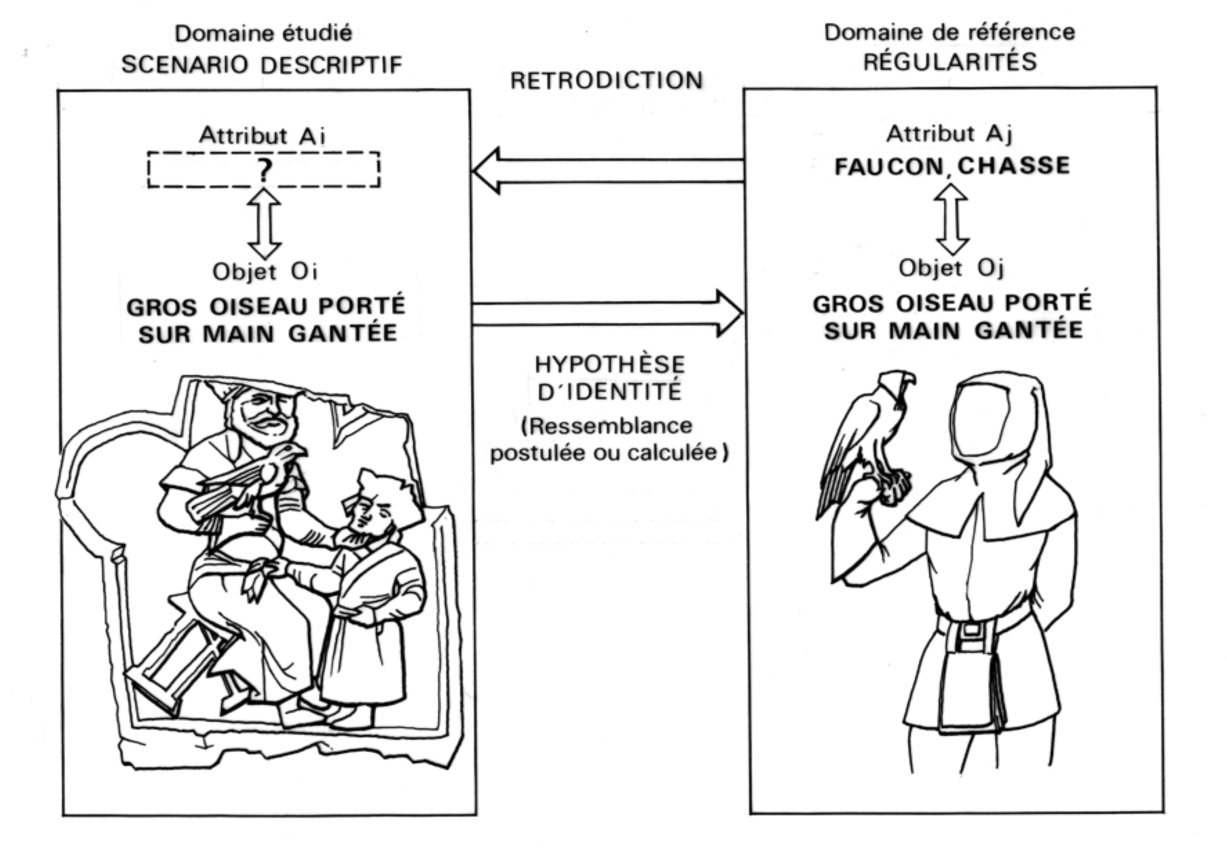
Fig. 1. Le mécanisme de l’interprétation selon J.-C. Gardin. L’interprétation des sources archéologiques procède par transfert d’attribut. L’exemple donné est celui de l’interprétation d’une stèle seldjoukide de Turquie qui représente sur un poing ganté, un gros oiseau. Le domaine de référence est ici la fauconnerie de Moyen Age (Gallay 1986, fig. 23. Inspiré de Gardin 1979, fig. 27 ; Roux 1971 ; Lagrange, Renaud 1987).

 

Question 3. La nécessité d’introduire des préconcepts sans définition (termes primitifs) à l’origine des chaînes de définitions des concepts (définitions descriptives) se retrouve-t-elle dans les chaînes d’inférence du logicisme ?

Nous écrivions : Les relations entre Oj et Aj du domaine de référence permettant l’interprétation d’un vestige ont été formulées de façon identique par référence à un troisième ensemble de faits. Il s’agit ici aussi d’un savoir construit et dans une certaine mesure contestable. Les domaines de référence forment donc des chaînes aux multiples maillons dont la structure est probablement extrêmement complexe et souvent très mal connue. Seuls certains segments, minuscules, en sont maîtrisés (fig. 2).

 

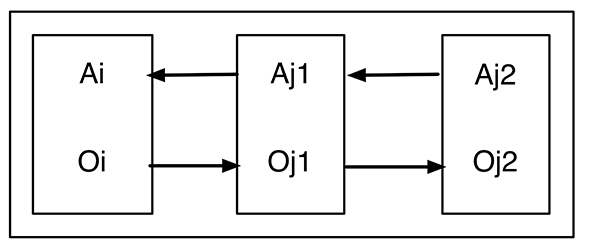
Fig. 2. Organisation des savoirs interprétatifs sous forme de chaînes de rétrodictions potentielles. L’interprétation de Oi nécessite l’établissement d’un référentiel Oj1 (propriété) -Aj1 (attribut). Mais ce dernier peut reposer lui-même sur un référentiel Oj2-Aj2. La chaîne peut ainsi être généralisée sans limites autres que celles imposées l’organisation pratique d’une recherche.

 

Il existe donc une certaine analogie entre le chaînage des définitions descriptives et le chaînage des corpus de références.

Constate-t-on, dans ce deuxième cas, les mêmes limites ?

1. Première analogie forte :

Dans les deux cas, la cohérence logique veut que l’on évite les cercles vicieux : dans le jeu des définitions, quand on tente de définir chacun des termes d’un système donné, il convient de ne jamais utiliser un terme dans un definiens qui ait été défini plus haut dans la chaîne. Dans le chaînage des transferts d’attribut, il conviendrait de même d’éviter ce type de retour en arrière.

2. Seconde analogie faible

La première analogie implique également que le chaînage des transferts d’attributs ne peut se déployer à l’infini, mais les causes de cette limitation ne sont pas les mêmes. Dans les sciences humaines, le transfert d’attribut est en effet fondé sur des connaissances culturelles et/ou historiques. Or nous vivons dans un monde fini, tant sur le plan chronologique que géographique. Les chaînes de comparaisons ne peuvent donc se développer à l’infini.

En résumé les définitions descriptives et stipulatives seraient plutôt en relation avec l’établissement des proposions Po correspondant à la base descriptive des démonstrations alors que les définitions opératoires sont spécifiquement liées aux dérivations de la construction et permettent de passer des propositions Po à la proposition terminale Pn (fig. 3).

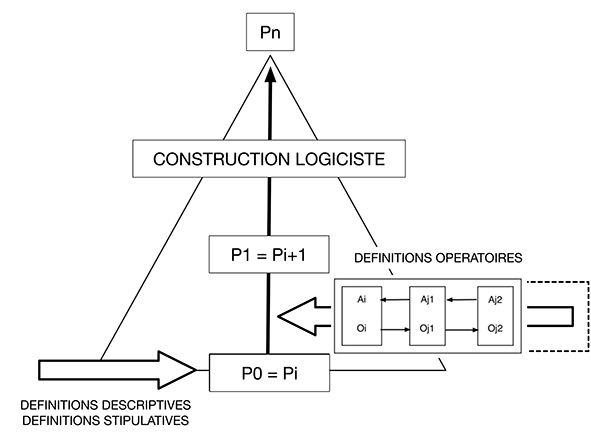
Fig. 3. Place des définitions de Hempel dans le déroulement d’une construction logiciste.

 

Références

 

BRIDGMAN P. W. 1927. The logic of modern physics. New York: Macmillan (YorkUniversity, Ontario Council university libraries, Toronto).

GALLAY A. 1986. L’archéologie demain. Paris : Belfond (Belfond sciences).

HEMPEL C. 2004 (2ème éd.). Éléments d’épistémologie. Paris : Armand Colin (Cursus).

LAGRANGE M.-S. RENAUD M. 1987. Cas n°6 : Superikon, essai de cumul de six expertises en iconographie In : Gardin, J.-C., Guillaume O. Herman P.O. et al. (éds). Systèmes experts et sciences humaines : le cas de l’archéologie.Paris : Eyrolles, p. 191-229.

ROUX J.-P. 1971. Essai d’interprétation d’un relief figuratif seldjoukide. Arts asiatiques,23, p. 41-49.